1.4电容和充电

电容和电荷

探索电容器如何储存电能涉及理解电容和电荷。我们从基本的电容概念开始，电容以法拉为单位进行测量，然后转向更详细的主题，如自电容和杂散电容，包括如何管理它们。讨论包括计算不同设置中电容的公式和介电材料的重要性。通过例子和理论，本指南解释了电容器如何充电和放电，给出了它们在电子电路中如何工作的完整图景。这桥接了理论和实际使用之间的差距。

电容

电容器的电容被定义为电容器在其内部存储最大电荷（Q）的能力。这里电荷以静电能量的形式存储。电容以基本的SI单位法拉进行测量。这些单位可能是微法拉、纳法拉、皮法拉或法拉。电容的表达式由下式给出：

C = $\frac{Q}{V}$ =$\frac{εA}{d}$ = ε0 * εr * $\frac{A}{d}$

在上述方程中：

• C是电容，
• Q是电荷，
• V是极板之间的电位差，
• A是极板之间的面积，
• d是极板之间的距离。
• ε是电介质的介电常数
• ε0是自由空间的介电常数
• εr是自由空间的相对介电常数

自电容

自电容特性与电容器特别是与孤立导体有关。正如名称所示，电容是孤立导体的属性，将其电位差提高到一伏特。通常，正常导体将具有互电容。这同样以SI单位法拉进行测量。

半径为‘R’的导体球的自电容由下式给出：

C=4 π * ε0 * R

一些标准设备的自电容值如下：

• 对于半径为20厘米的范德格拉夫发生器的顶部金属板，自电容为22.24 pF。

• 对于地球，自电容为710 uF。

杂散电容

杂散电容是不需要的电容。电容器在电路中引入一些电容。但是，像电阻器、电感器甚至电线这样的元件也会有一些电容。这被称为杂散电容。通常在高频下，这会向电路引入噪声。除非导体在长距离上彼此靠近或面积很大，否则这种不需要的电容很小。

杂散电容不能完全消除，但可以减少。电路设计人员在设计电路时应考虑杂散电容。为了减少不需要的电容，应保持元件和线路之间的分离。

它也以SI单位法拉进行测量。

例子包括线圈匝之间的电容，两个相邻导体之间的电容。

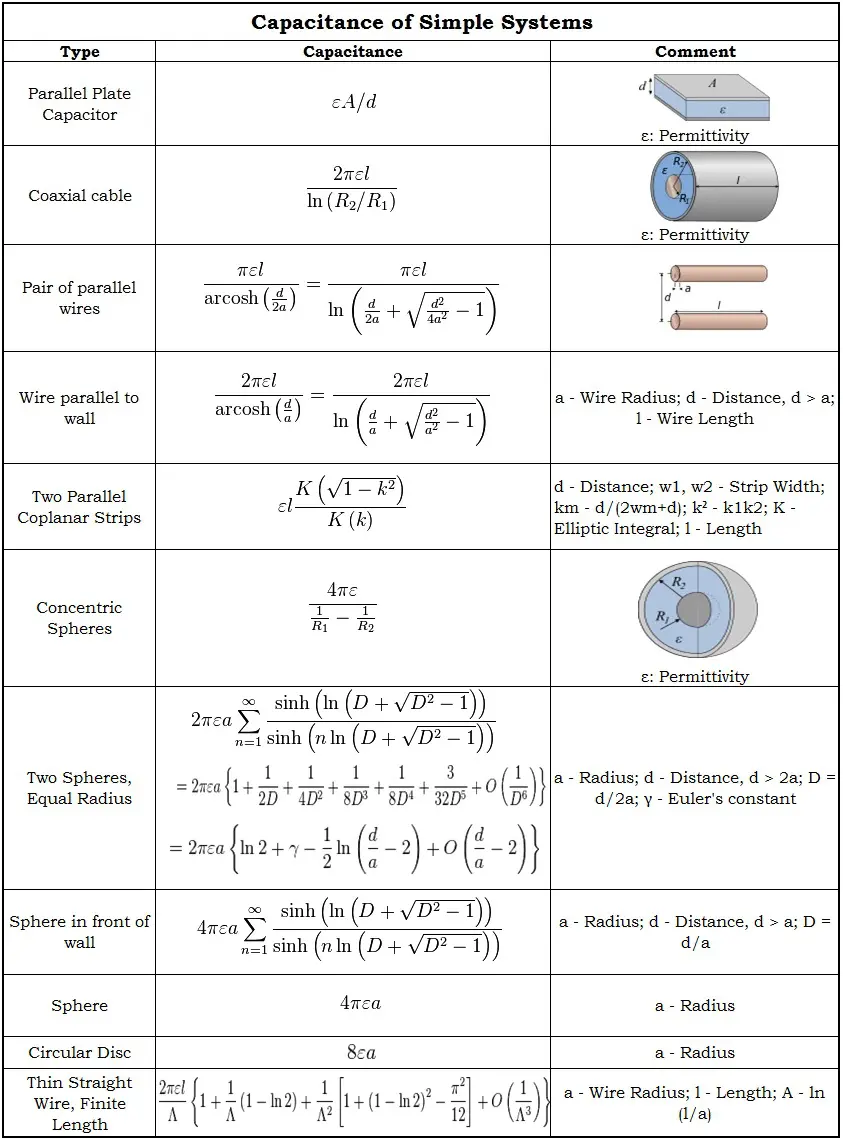
简单系统的电容

计算电容无非是求解拉普拉斯定理∇ 2φ = 0，电容器表面的电位恒定。一些简单系统的电容值和方程如下给出。

电容器上的电荷

电容器在其金属极板上储存最大电荷（Q）的能力称为其电容值（C）。储存的电荷的极性可以是负的或正的。例如，电容器的一个极板上有正电荷（+ve），另一个极板上有负电荷（-ve）。电荷、电容和电压的表达式如下。

C = Q/V, Q = CV, V = Q/C

因此，电容器的电荷与其电容值和极板之间的电位差成正比。电荷以库仑为单位进行测量。

一库仑：

一库仑的电荷可以定义为在两个导体之间具有1法拉电容并在1伏电压下运行的电容器。

以空气为电介质

具有电容C、电位差“V”和空气作为电介质的电容器中储存的电荷“Q”由下式给出，

Q = CV = $\frac{(ε * (A * V))}{d}$

以固体为电介质

具有固体作为电介质的电容器的电荷“Q”由下式给出，

Q = CV = $\frac{(ε0 * εr * (A * V))}{d}$

其中

• ε0是自由空间的介电常数，
• εr是电介质材料的相对介电常数，
• ε是电介质材料的介电常数。

从上述两种情况我们可以观察到

电容器的电荷与极板的面积、极板之间电介质的介电常数成正比，与极板之间的分离距离成反比。

因此，极板的面积越大，电荷就越多，极板之间的分离距离越大，电容器上的电荷就越少。

平行板电容器

图1.平行板电容器电路

上图展示了平行板电容器电路。正如我们所知，电容与极板的面积（A）成正比，与两个金属极板之间的分离距离（d）成反比。平行板电容器的电容值由下式给出：

​C = k * ε0 * $\frac{A}{d}$

其中，k 是介电常数，ε0是自由空间的介电常数，其值为 8.854×10−12 F/m。介电常数（k）是与电介质材料相关的参数，与空气相比，它增加了电容。极板的表面积越大，电容值越大；极板之间的分离距离越大，电容值越小。另一个平行板电容器电路的例子如下图所示。

图2.平行板电容器

电容示例1

现在我们将计算一个平行板电容器的电容值，该电容器的极板表面积为200平方厘米，极板之间的距离为0.4厘米，使用空气作为电介质。

我们知道平行板电容器的电容公式为：

C = εA/d 其中 ε=8.854×10^−12 F/m A=200cm2=0.02m2 D=0.4cm=0.004m C = 8.854 X 10^-12 * (0.02 m2/0.004m) = 44.27 pF

因此，这个平行板电容器的电容值为44.27皮法拉。

电容器的充电与放电

下面的电路用于解释电容器的充电和放电特性。假设电路中所示的电容器完全放电。在这个电路中，电容器的电容值为100微法拉，施加到电路的电源电压为12伏特。

现在，将连接到电容器的电路中的开关移动到点A。然后，电容器开始以充电电流（i）充电，并且这个电容器完全充电。当电容器完全充电时，电容器两端的充电电压等于电源电压，即 VS=VC=12V。当电容器完全充电意味着即使将电源电压从电路中断开，电容器也能保持恒定的电压充电。

在理想电容器的情况下，电荷在电容器上保持恒定，但在普通电容器的情况下，完全充电的电容器会因为其漏电流而缓慢放电。

图：充电和放电电容器电路

当开关移动到位置B时，电容器通过连接在电路中的灯泡缓慢放电。最终，电容器完全放电至零。当电容器完全充电时，灯泡最初会非常亮，但随着电容器上的电荷减少，灯泡的亮度也会降低。

电容充电示例2

现在让我们计算上述电路中电容器的电荷。我们知道，电容器的电荷公式为：

Q=CV 其中，C=100μF V=12V 将这些值代入上述公式，我们得到： Q = 100uF*12V=1.2mC 因此，上述电路中电容器的电荷为1.2毫库仑（mC）。

通过电容器的电流

流经任何电路的电流是单位时间内通过它的电荷（Q）的速率。但电容器上的电荷与施加在其上的电压成正比。电容器的电荷、电流和电压之间的关系由以下方程给出：

I (t) = d Q(t)/dt = C dV(t)/dt ​ 我们知道：

Q=CV

V = Q/C ​ V (t) = Q(t)/C

Q(t) =C V(t) 电容器的电流与电压的关系为：Q(t) =C V(t)

从这个关系中，我们观察到流经电路中电容器的电流是电容和施加电压变化率的乘积。流经电容器的电流与电容器的电容成正比，与电压变化率成正比。

电流越大，电路的电容越大；施加的电压越高，流经电路的电流越大。如果电压恒定，则电荷也恒定。因此没有电荷流动。所以流经电路的电流将变为零。

电容单位（法拉）

1861年，约西亚·拉蒂默·克拉克（Josiah Latimer Clark）首次使用了“法拉”这一术语。法拉是电容的标准单位。这是一个非常大的单位。

1法拉的电容定义为1库仑的电荷在1伏特电压下运行的电容。

C = Q/V ​ 1Farad = 1Coluomb/1Volt ​ 如今，市面上有电容值高达数百法拉的电容器。这些电容值高的电容器被称为“超级电容器”。这些超级电容器利用大面积来提供高能量，因为它们具有高电容值。

在低电压下，超级电容器能够以高电容值储存高能量。这些高能量超级电容器用于手持便携设备中，以替代大型、沉重且昂贵的锂电池，因为它们像电池一样储存高能量。这些电容器还用于车辆中的音频和视频系统，替代高电压电池。

法拉的子单位

电容的标准单位是法拉。但通常这是一个较大的测量单位。法拉有一些子单位，它们是微法拉（uF）、纳法拉（nF）和皮法拉（pF）。

这些子单位与法拉的关系如下：

1micro-Farad (uF) = (1/1000000) F = 10^-6 F

1nano-Farad (uF) = (1/1000000000) F = 10^-9 F

1pico-Farad (uF) = (1/1000000000000) F = 10^-12 F

现在我们来看一些电容子单位之间的转换：

(i) 将33 pF转换为nF：33pF=0.033nF

(ii) 将22 nF转换为uF：22nF=0.022uF

(iii) 将11 uF转换为F：11uF=0.011F

电容器中的能量

能量是克服电场对电容器进行完全充电所需的功。在电容器充电的初始阶段，电荷Q在极板之间从一个极板转移到另一个极板。这个电荷（+Q或-Q）在电容器的两个极板之间相互交换。在转移一些电荷后，极板之间形成了一个电场，此时我们需要额外的功来完全充电电容器。这个额外的功称为电容器中储存的能量。能量以焦耳（J）为单位进行测量。现在我们来看能量和功的方程。

dW = V dQ dW = (Q/C) dQ After integration of the above equation is, W = Q^2/2C W = (CV)^2/2C W= CV^2/2 焦耳 最终我们得到电容器中储存的能量为： 最终我们得到电容器中储存的能量为：

Energy (W) = CV^2/2 焦耳

现在我们计算一个电容值为200 uF、工作电压为12V的电容器中储存的能量。

W = CV^2/2 W = (200×10^-6×12^2)/2 = 14.4 mJ